Prof. Horstmann and nuclear Fusion & Fission, Enrichment Uranium and Nuclear Power Plant

Introduction to Fusion
The appeal of fusion … Nuclear fusion as a means of energy generation is very appealing. The products of fusion are generally not radioactive and therefore fusion is a ‘greener’ process than fission. A fusion reaction of particular appeal to nuclear scientists is the reaction between the two heavier isotopes of hydrogen – deuterium (hydrogen-2) and tritium (hydrogen-3).
The potential fusion reaction between these Isotopes is represented as:
The current difficulty with fusion is the high temperature needed to overcome the electrostatic repulsion between nuclei. Not only is it very difficult to achieve these high temperatures, but finding materials to contain such high temperatures is also a challenge.
Intoduction to Fission
Chadwick’s discovery of the neutron, opened new avenues of research into reactions. The fact that neutrons had no charge encouraged their use in bombarding the nuclei of atoms. The idea was that if the nucleus of an atom of a particular element could absorb an extra neutron, then a different isotope of that element should be produced.
Neutron bombardment of uranium was also considered to be a way of producing elements heavier than uranium – the trans-uranium elements.
Otto Hahn, Fritz Strassmann and Lise Meitner worked together on the neutron bombardment of uranium in Germany in the 1930s. Eventually Meitner, being Jewish, had to flee Germany and went to work with Bohr.
Hahn and Strassmann continued to work on the neutron bombardment of uranium (atomic number 92) and were stunned to discover barium (atomic number 56) as a product of this bombardment.
Within weeks, it was discovered that neutrons were also released during the fission of uranium and that these neutrons could cause the splitting of more uranium nuclei and lead to a chain reaction.
The first step in the fission of uranium-235 involves the formation of unstable U-236 nuclei by bombardment with neutrons.
Each unstable U-236 nucleus breaks down into a Kr-97 nucleus and a Ba-137 nucleus accompanied by the release of three neutrons.

Simple animation of nuclear fission. Firstly, a neutron is about to be captured by the nucleus of a U-235(yellow center) atom and U-238(grey center) atom. Secondly, the neutron has been absorbed and briefly turned the nucleus into a highly excited U-236 atom and U-239 atom. Thirdly, the U-236 atom fission, resulting in two fission fragments (Barium and Krypton) and three neutrons, all with large amounts of kinetic energy. Plutonium-239 results from U-239. Skip this part, continue reading below.
Consider the uranium 235 fission reaction (animation above). Fission is initiated by the absorption of a slow moving neutron, which creates an excited uranium 236 nucleus. This nucleus is unstable, because similar to a growing liquid drop when a nucleus gets too large its outer nuclei have fewer neighboring ones to keep them whole nucleus in one large mass. (From the point of view of the binding energy, their binding energy is lower than what it would have been were the nucleons had been part of a smaller nucleus – remember that the binding energy per nucleon drops for these large nuclei.) In a too large a liquid drop the breakup results in formation of smaller droplets and not just the departure of separate surface molecules. Similarly, in nuclear fission the excited uranium 236 breaks into smaller nuclei; typically a krypton nucleus, a barium nucleus and three neutrons. The combined mass of these « parts » is less than the mass of the mother nucleus. This missing mass is released in the form of kinetic energy of the decay elements (the krypton, barium, and the three neutrons).
The above reaction is not the only possibility, however. Again, as in the liquid drop analogy, the uranium 236 could instead break into a xenon, a strontium, and two neutrons. Which of these two separate reactions will be the fate of a given uranium 236 nucleus could only be determined statistically. So, the energy and the number of the neutrons is statistical. Despite this statistical variation in a typical fission reaction about roughly 200 MeV of energy is released per single fission decay. This energy is distributed, roughly, in the following manner:
- 170 MeV to kinetic energy of the fission fragments
- 5 MeV to kinetic energy of neutrons
- 25 MeV to b-decay and g-rays
The role of any device that is designed for using fission energy is to extract the kinetic energy of the by products and to slow down the neutrons so that they in turn initiate further fission reactions and thus sustain a chain reaction. As the fission fragments collide with other surrounding nuclei they exchange kinetic energy and thus generate heat. In the case of power generating devices a heat exchange material, such as water, can carry away this heat and use it to generate steam. The steam can then mechanically turn a motor to generate electricity or to just turn a propeller. In the case of a bomb this energy is practically let loose to do damage. As for the neutrons, they can be slowed to velocities that could result in capture by other uranium 236 nuclei by making them collide with other nuclei first. These are called moderators. An ideal moderator must slow down the neutrons without absorbing them. Hydrogen is an excellent choice for slowing down the neutrons, but it is also a very good absorber! So, it is not a good moderator. Deuterium, on the other hand satisfies both criteria. So, one of the moderators used in reactors is heavy water. In heavy water the two hydrogen atoms of water molecule are in instead deuterium atoms. Other moderators are beryllium (Be) and graphite (carbon, 12C). As we have already discussed Control rods, often made of cadmium that is an effective neutron absorber, are brought near the fission material to affect the rate of the chain reaction, and thus control the rate of extracting energy form the uranium fuel.
1. Uranium – 92-U-235
Spin and half-life
Level energy(keV) Spin & Parity Half-life
-------------------------------------------------
ground state 7/2- 703.8E+6Y 5
7.50000E-02 1/2+ 25M
Mass (taken from Audi et al. (April 2011))
235.043931368 ± 0.000001962 (amu) [mass excess = 40921.807 ± 1.828 (keV) ]
Beta-decay energy (calculated as M(A,Z)-M(A,Z+1), taken from Audi et al. (April 2011))
-124.033 ± 0.855 (keV)
Strong Gamma-rays from Decay of U-235 (Compiled from ENSDF as of March 2011)
[ Iintensities before May 23th of 2013 were values when total intensity of the decay mode was 100(%) and a branching ratio of each decay mode was not multiplied. ]
γ-ray energy(keV) Intensity(%) Decay mode / Half-life
----------------------------------------------------------
143.76 10.96 Alpha 703.8E+6 Y
163.33 5.08 Alpha 703.8E+6 Y
185.72 57.2 Alpha 703.8E+6 Y
----------------------------------------------------------
*: relative, ~ approximate, ? calculated or estimatted
>: greater than or equal to, <: less than or equal to
[ Intensities; total intensity of the nuclide is 100(%). ]
Decay data
Decay mode Half-life
A 703.8E+6 Y 5
Cross Sections
Table of cross sections, U-235.
Figures of cross sections, U-235: type-1: type-2: type-3.
type-1: total, elastic and inelastic scattering, capture and fision cross sections
type-2: same as type-1 but cross sections are averaged in 70 energy group intervals
type-3: threshold reaction cross sections
Parent Nuclides by Reactions
U -234 (Z= 92, A=234), MT=102 (n,γ)
U -235 (Z= 92, A=235), MT= 2 (Elastic scattering)
U -235 (Z= 92, A=235), MT= 4 (Inelastic scattering)
U -236 (Z= 92, A=236), MT= 16 (n,2n)
U -237 (Z= 92, A=237), MT= 17 (n,3n)
U -238 (Z= 92, A=238), MT= 37 (n,4n)
2. Uranium – 92-U-236
Spin and half-life
Level energy(keV) Spin & Parity Half-life
-------------------------------------------------
ground state 0+ 2.342E+7Y 4
Mass (taken from Audi et al. (April 2011))
236.045569468 ± 0.000001966 (amu) [mass excess = 42447.687 ± 1.832 (keV) ]
Beta-decay energy (calculated as M(A,Z)-M(A,Z+1), taken from Audi et al. (April 2011))
-925.733 ± 50.410 (keV)
Strong Gamma-rays from Decay of U-236 (Compiled from ENSDF as of March 2011)
[ Iintensities before May 23th of 2013 were values when total intensity of the decay mode was 100(%) and a branching ratio of each decay mode was not multiplied. ]
γ-ray energy(keV) Intensity(%) Decay mode / Half-life
----------------------------------------------------------
49.46 0.08 Alpha 2.342E7 Y
112.79 0.02 Alpha 2.342E7 Y
171.15 6.E-05 Alpha 2.342E7 Y
----------------------------------------------------------
*: relative, ~ approximate, ? calculated or estimatted
>: greater than or equal to, <: less than or equal to
[ Intensities; total intensity of the nuclide is 100(%). ]
Decay data
Decay mode Half-life
A 2.342E7 Y 4
Cross Sections
Table of cross sections, U-236.
Figures of cross sections, U-236: type-1: type-2: type-3.
type-1: total, elastic and inelastic scattering, capture and fission cross sections
type-2: same as type-1 but cross sections are averaged in 70 energy group intervals
type-3: threshold reaction cross sections
Parent Nuclides by Reactions
U -235 (Z= 92, A=235), MT=102 (n,γ)
U -236 (Z= 92, A=236), MT= 2 (Elastic scattering)
U -236 (Z= 92, A=236), MT= 4 (Inelastic scattering)
U -237 (Z= 92, A=237), MT= 16 (n,2n)
U -238 (Z= 92, A=238), MT= 17 (n,3n)
3.1 Krypton – 36-Kr-97
Spin and half-life
Level energy(keV) Spin & Parity Half-life
-------------------------------------------------
ground state 63MS 4
Mass (taken from Audi et al. (April 2011))
96.949088785 ± 0.000140000 (amu) [mass excess = -47423.491 ± 130.409 (keV) ]
Beta-decay energy (calculated as M(A,Z)-M(A,Z+1), taken from Audi et al. (April 2011))
11094.713 ± 130.517 (keV)
– Neutron-induced Fission Yields (from main actinide nuclides) – Independent Fission Yield –
Product Nuclide Energy Fission Yield Uncertainty(1σ)
-----------------------------------------------------------
Kr- 97 U-235 Thermal 2.965250e-07 1.897750e-07
Kr- 97 U-235 Fast 1.147610e-06 7.344730e-07
Kr- 97 U-235 High 1.071020e-06 6.854520e-07
Kr- 97 U-238 Fast 8.015780e-06 5.130100e-06
Kr- 97 U-238 High 1.499330e-05 9.595720e-06
Kr- 97 Pu-239 Thermal 1.606670e-05 1.028270e-05
Kr- 97 Pu-239 Fast 1.219740e-07 7.806360e-08
Kr- 97 Pu-239 High 5.559590e-07 3.558140e-07
Kr- 97 Pu-241 Thermal 5.550760e-07 3.552490e-07
Kr- 97 Pu-241 Fast 1.199060e-06 7.674000e-07
-----------------------------------------------------------
Thermal=0.0253eV, Fast=500keV(Fast reactor spectrum), High=14MeV
– Neutron-induced Fission Yields (from main actinide nuclides) – Cumulative Fission Yield –
Product Nuclide Energy Fission Yield Uncertainty(1σ)
-----------------------------------------------------------
Kr- 97 U-235 Thermal 2.965280e-07 1.897790e-07
Kr- 97 U-235 Fast 1.147630e-06 7.344820e-07
Kr- 97 U-235 High 1.071470e-06 6.847240e-07
Kr- 97 U-238 Fast 8.022990e-06 5.132830e-06
Kr- 97 U-238 High 1.499630e-05 9.587250e-06
Kr- 97 Pu-239 Thermal 1.606740e-05 1.028320e-05
Kr- 97 Pu-239 Fast 1.219800e-07 7.806720e-08
Kr- 97 Pu-239 High 5.563600e-07 3.558400e-07
Kr- 97 Pu-241 Thermal 5.550890e-07 3.552000e-07
Kr- 97 Pu-241 Fast 1.199100e-06 7.674210e-07
-----------------------------------------------------------
Thermal=0.0253eV, Fast=500keV(Fast reactor spectrum), High=14MeV
3.2 Barium – 56-Ba-137
Spin and half-life
Level energy(keV) Spin & Parity Half-life
-------------------------------------------------
ground state 3/2+ Stable
6.61659E+02 11/2- 2.552M 1
Mass (taken from Audi et al. (April 2011))
136.905827046 ± 0.000000364 (amu) [mass excess = -87721.542 ± 0.339 (keV) ]
Beta-decay energy (calculated as M(A,Z)-M(A,Z+1), taken from Audi et al. (April 2011))
-615.489 ± 12.212 (keV)
Strong Gamma-rays from Decay of Ba-137 (Compiled from ENSDF as of March 2011)
[ Iintensities before May 23th of 2013 were values when total intensity of the decay mode was 100(%) and a branching ratio of each decay mode was not multiplied. ]
γ-ray energy(keV) Intensity(%) Decay mode / Half-life
----------------------------------------------------------
661.66 89.9 IT 2.552 M
----------------------------------------------------------
*: relative, ~ approximate, ? calculated or estimatted
>: greater than or equal to, <: less than or equal to
[ Intensities; total intensity of the nuclide is 100(%). ]
Decay data
Decay mode Half-life
IT 2.552 M 1
Cross Sections
Table of cross sections, Ba-137.
Figures of cross sections, Ba-137: type-1: type-2: type-3.
type-1: total, elastic and inelastic scattering, capture and fission cross sections
type-2: same as type-1 but cross sections are averaged in 70 energy group intervals
type-3: threshold reaction cross sections
Parent Nuclides by Reactions
Ba-136 (Z= 56, A=136), MT=102 (n,γ)
Ba-137 (Z= 56, A=137), MT= 2 (Elastic scattering)
Ba-137 (Z= 56, A=137), MT= 4 (Inelastic scattering)
Ba-138 (Z= 56, A=138), MT= 16 (n,2n)
La-138 (Z= 57, A=138), MT= 28 (n,np)
La-138 (Z= 57, A=138), MT=104 (n,d)
La-139 (Z= 57, A=139), MT= 32 (n,nd)
La-139 (Z= 57, A=139), MT=105 (n,t)
Ce-140 (Z= 58, A=140), MT=107 (n,α)
Ce-141 (Z= 58, A=141), MT= 22 (n,nα)
– Neutron-induced Fission Yields (from main actinide nuclides) – Independent Fission Yield –
Product Nuclide Energy Fission Yield Uncertainty(1σ)
-----------------------------------------------------------
Ba-137 U-235 Thermal 5.479180e-07 3.506670e-07
Ba-137 U-235 Fast 2.233520e-07 1.429460e-07
Ba-137 U-235 High 3.851810e-05 2.465160e-05
Ba-137 U-238 Fast 2.333680e-08 1.493560e-08
Ba-137 U-238 High 1.003490e-06 6.422380e-07
Ba-137 Pu-239 Thermal 1.866410e-05 1.194500e-05
Ba-137 Pu-239 Fast 1.448370e-05 9.269590e-06
Ba-137 Pu-239 High 1.655660e-04 1.059620e-04
Ba-137 Pu-241 Thermal 6.432390e-07 4.116730e-07
Ba-137 Pu-241 Fast 6.501730e-07 4.161110e-07
-----------------------------------------------------------
Ba-137m U-235 Thermal 1.322110e-06 8.461470e-07
Ba-137m U-235 Fast 6.258950e-07 4.005730e-07
Ba-137m U-235 High 1.766670e-04 1.130670e-04
Ba-137m U-238 Fast 6.539620e-08 4.185360e-08
Ba-137m U-238 High 4.602610e-06 2.945670e-06
Ba-137m Pu-239 Thermal 4.503590e-05 2.882290e-05
Ba-137m Pu-239 Fast 4.058740e-05 2.597590e-05
Ba-137m Pu-239 High 7.593840e-04 4.860060e-04
Ba-137m Pu-241 Thermal 1.552120e-06 9.933540e-07
Ba-137m Pu-241 Fast 1.821970e-06 1.166060e-06
-----------------------------------------------------------
Thermal=0.0253eV, Fast=500keV(Fast reactor spectrum), High=14MeV
– Neutron-induced Fission Yields (from main actinide nuclides) – Cumulative Fission Yield –
Product Nuclide Energy Fission Yield Uncertainty(1σ)
-----------------------------------------------------------
Ba-137 U-235 Thermal 6.175470e-02 3.357740e-04
Ba-137 U-235 Fast 6.206910e-02 2.621760e-04
Ba-137 U-235 High 4.954390e-02 1.386880e-03
Ba-137 U-238 Fast 6.050980e-02 4.239710e-04
Ba-137 U-238 High 5.150780e-02 1.030170e-03
Ba-137 Pu-239 Thermal 6.611160e-02 3.317270e-04
Ba-137 Pu-239 Fast 6.587770e-02 3.303470e-04
Ba-137 Pu-239 High 4.547960e-02 2.727500e-03
Ba-137 Pu-241 Thermal 6.649210e-02 4.658690e-04
Ba-137 Pu-241 Fast 6.378910e-02 1.279800e-03
-----------------------------------------------------------
Ba-137m U-235 Thermal 5.848130e-02 2.991100e-04
Ba-137m U-235 Fast 5.877930e-02 3.039430e-04
Ba-137m U-235 High 4.689030e-02 1.874390e-03
Ba-137m U-238 Fast 5.730270e-02 5.743870e-04
Ba-137m U-238 High 4.877720e-02 1.366250e-03
Ba-137m Pu-239 Thermal 6.259230e-02 3.154850e-04
Ba-137m Pu-239 Fast 6.237460e-02 4.384970e-04
Ba-137m Pu-239 High 4.294450e-02 3.430980e-03
Ba-137m Pu-241 Thermal 6.296750e-02 4.433090e-04
Ba-137m Pu-241 Fast 6.040780e-02 2.416770e-03
-----------------------------------------------------------
Thermal=0.0253eV, Fast=500keV(Fast reactor spectrum), High=14MeV
Nuclear fission can take place spontaneously or it can be induced by bombarding an atomic nucleus with moving particles such as neutrons, protons or alpha particles or with electromagnetic radiation in the form of gamma rays. It occurs most readily with heavy elements such as uranium and plutonium. The two nuclei formed as a result of this bombardment are both positively charged and repel each other.
The fission of one kilogram of uranium releases as much energy as is obtained from burning approximately 3 000 tonnes of coal.
It was mentioned earlier that, as well as new nuclei, several neutrons are formed from the fission of uranium. These neutrons can strike other uranium nuclei, which then release more neutrons. The extra neutrons can then split further uranium nuclei, and so the process goes on and can be self-sustaining in what is known as a chain reaction. Then destructive power of such a fission reaction was exploited in the atomic bombs used to end the Second World War. Today we see constructive applications in nuclear reactors, which effectively harness the fission process for electricity generation. Nuclear fission is the basis of all existing nuclear power stations.
FISSION AND FUSION
LA FISSION ET LA FUSION
![]()

1. FISSION – LA FISSION
Process through which an atomic nucleus splits into two approximately equal parts with the release of large amounts of energy.
Fission has been observed for many nuclei of mass number A greater than 200 (eg, uranium 233, plutonium-239) and can be caused by neutrons, photons, electrons, protons, deuterons and alpha particles .
The first fission was discovered that uranium bombarded by neutrons. With thermal neutrons, the effect is due to uranium 235, only present in natural uranium at a rate of 1 atom for 139 238 atoms.
Processus par lequel un noyau d’atome se brise en deux parties approximativement égales avec dégagement d’une grande quantité d’énergie.
La fission a été observée pour beaucoup de noyaux de nombre de masse A supérieur à 200 (ex. uranium 233, plutonium 239) et elle peut être engendrée par des neutrons, des photons, des électrons, des protons, des deutons et des particules alpha.
Le premier phénomène de fission découvert fut celui de l’uranium bombardé par des neutrons. Avec des neutrons thermiques, l’effet est dû à l’uranium 235, présent seulement dans l’uranium naturel, à raison de 1 atome pour 139 atomes d’uranium 238.

At the same time as the larger fragments, neutrons are released during fission. With these free neutrons, the fission reaction can become, in certain conditions, self-sustaining and lead to continuous production of energy. This is the basic operation of the reactors.
The fission of uranium 235 with neutrons produces a thermal energy of about 200 MeV.
About 85% of this energy appears as kinetic energy (energy due to the speed of a moving body) of fission products and ultimately results in heat generation. Yet this enormous energy represents only 0.1% of the mass energy contained in a heavy nucleus. In other words, the energy release comes from a weight loss of 1 in 1000, and this according to the Einstein relation.

Albert EINSTEIN
En même temps que les gros fragments, des neutrons sont libérés durant la fission. Grâce à ces neutrons libres, la réaction de fission peut devenir, dans certaines conditions favorables, autoentretenue et conduire ainsi à une production continue d’énergie. C’est la base du fonctionnement des réacteurs.
La fission de l’uranium 235 par des neutrons thermiques produit une énergie d’environ 200 MeV.
Environ 85% de cette énergie apparaît sous forme d’énergie cinétique (énergie due à la vitesse d’un corps en mouvement) des produits de fission et se traduit finalement par un dégagement de chaleur. Cette énergie pourtant énorme ne représente cependant que 0.1% de l’énergie de masse contenue dans un noyau lourd. Autrement dit, le dégagement d’énergie provient d’une perte de masse de 1 pour 1000, et ce d’après la relation d’Einstein.

Prof. HORSTMANN
If one could split all the atoms in one kilogram of uranium-235 would produce an energy equal to that provided by three million kilograms of coal. However, we saw that natural uranium contains only a small proportion of uranium 235.
To get closer to the theoretical complete combustion of all the atoms in the uranium is used batteries or regenerative incubators in which the fertile material produces more fuel than it is burned.
For the chain reaction takes an explosive nature, it is necessary to have a certain amount of uranium 235, is the critical mass.
To make a bomb, we calculate the sub-critical masses, combined into one critical mass to trigger the explosion.
Si l’on pouvait fissionner tous les atomes de 1 kilogramme d’uranium 235, on obtiendrait une énergie égale à celle fournie par 3 millions de kilogrammes de charbon. Toutefois, nous avons vu que l’uranium naturel ne contient qu’une faible proportion d’uranium 235. Afin de se rapprocher de la combustion théorique complète de tous les atomes contenus dans l’uranium, on utilise des piles régénératrices ou couveuses dans lesquelles la matière fertile produit plus de combustible qu’il n’en est brûlé.
Pour que la réaction en chaîne prenne un caractère explosif, il est nécessaire qu’il y ait un certain quantité d’uranium 235, c’est la masse critique.
Pour réaliser une bombe A, on calcule des masses sous-critiques, réunies en une seule masse critique pour déclencher l’explosion.
2. FUSION – LA FUSION
By merging the nuclei of lighter elements, it causes the formation of nuclei of heavy atoms with energy production.
For the fusion reaction to occur, it is necessary that the nuclei in the presence approaching at a distance comparable to the nuclear radius. It must then overcome the mutual electrostatic repulsion of the nuclei and connect speeds. It achieves this by carrying considerable kinetic energy kernels to the internal temperature of the sun. (Solar power is also the result of a fusion reaction.)
In the thermonuclear bomb, the temperature required by the reaction (about 5 million degrees) is provided by the previous explosion of a bomb A.
In the industrial sector would require the energy released by fusion is greater than the energy used for heating gas. It therefore seeks the means of producing temperatures never reached before in the industry.
We can use deuterium (D or 21H), a natural isotope of hydrogen whose nucleus (deuteron) is a shot used in accelerators. Deuterium is the basis of heavy water.
Par la fusion des noyaux des éléments les plus légers, on provoque la formation de noyaux d’atomes lourds avec production d’énergie.
Pour que la réaction de fusion se produise, il faut que les noyaux en présence s’approchent à une distance comparable au rayon nucléaire. Il faut surmonter alors la répulsion électrostatique mutuelle des noyaux et leur communiquer des vitesses élevées. On réalise ces énergies cinétiques considérables en portant les noyaux à la température interne du soleil. (L’énergie solaire est d’ailleurs le résultat d’une réaction de fusion.)
Dans la bombe thermonucléaire, la température nécessitée par la réaction (de l’ordre de 5 millions de degrés) est fournie par l’explosion préalable d’une bombe A.
Dans le domaine industriel, il faudrait que l’énergie libérée par la fusion soit supérieure à l’énergie employée pour l’échauffement du gaz. On cherche donc les moyens de produire des températures jamais atteintes jusqu’alors dans l’industrie.
On peut utiliser le deutérium (D ou 21H), élément naturel isotope de l’hydrogène et dont le noyau (deuton) est un projectile utilisé dans les accélérateurs. Le deutérium est à la base de l’eau lourde.
The energy released by fusion of all atoms in one gram of deuterium gas, equivalent to the energy released by burning about 2.8 million kilograms of coal.
We may also use tritium (T ou31H) radio-isotope of hydrogen, whose nucleus is the tritone. The fusion reactions leading to helium He.
Deuterium is a constituent of ordinary water (1 / 5000), the water of all seas represent the energy point of view, the possibility of life 10 billion years with the current energy consumption.
L’énergie libérée par la fusion, de tous les atomes contenus dans 1 gramme de gaz deutérium, équivaut à l’énergie libérée par la combustion d’environ 2 800 000 kilogrammes de charbon.
On peut également employer le tritium (T ou31H) radio-isotope de l’hydrogène, dont le noyau est le triton. Les réactions de fusion aboutissent à l’hélium He.
Le deutérium étant un élément constitutif de l’eau ordinaire (1/5000), l’eau de l’ensemble des mers représenterait au point de vue énergétique, la possibilité de vivre 10 milliards d’années avec la consommation actuelle d’énergie.
3. Enrichment Uranium
Introduction Enrichment Uranium
First of all lets look at two way’s uranium enrichment: the gas centrifuge, which promises vast efficiency improvements and far less power consumption than the previous way (gas diffusion) enrichment.

CANDU Nuclear Power Plant at Qinshan, China
Enrichment, part 1.
“Enrichment” or more particularly “uranium enrichment” is probably one of those phrases that the average person hears on television or reads on the Internet and has only the vaguest concept of what it means. They likely think “it’s bad” and “it has something to do with uranium, which I think is bad, for some reason”. Commentators and journalists decry the idea that Iran *gasp* might have access to uranium enrichment. Our leaders both domestic and international, loudly thunder that lesser nations shall not be allowed to develop enrichment.
Iranian enrichment President Iranian, Mahmoud Ahmadinejad
The world of the nucleus is a secret world, shielded from everything else by the cloud of electrons surrounding it. The electrons do all of the interacting, the nucleons do nearly nothing. The only hint they give to their existence is their charge, which is balanced by the electrons, and their mass. Practically all of the mass of the atom is in the nucleus.
Different isotopes of elements have different masses. They have the same number of protons, and hence the same charge and the same chemical nature, but different masses. From a chemical perspective, there’s no difference between most isotopes (with a few exceptions, like normal hydrogen and deuterium). But from a nuclear perspective there can be a huge difference between two naturally occurring isotopes. Lithium is a good example. Natural lithium is 90% lithium-7 and about 10% lithium-6. Chemically they’re the same. You can make batteries from lithium-6 just as well as you can make batteries from lithium-7. But from a nuclear perspective, they’re really, really different. Lithium-7 has almost no appetite to absorb neutrons, whereas lithium-6 has a HUGE appetite to absorb neutrons.
Uranium is in an analogous situation. Uranium-235 and uranium-238 are the two naturally occurring isotopes of uranium. One of them is far more common than the other. Can you guess which? Yeah, it’s the one that we’re not so interested in. Kind of like how when your toast falls down it always seems to land on the buttered side. Nevertheless, we’re a lot more interested in uranium-235, which is only 71 out of every 10000 uranium atoms than we are about uranium-238, which is the other 9920 out of 10000 uranium atoms. (1 atom out of 10000 is uranium-234, but we won’t worry about that right now).
Enrichment is the process where you separate one kind of isotope from another, and the overwhelming reason to do it is because you intend to use your product in a nuclear process. Because if you want to do a chemical process, you usually don’t care too much about what kind of isotope mix you have. Sometimes, but very rarely.
So how do you conduct enrichment? Well, your toolbox is pretty sparse. All of the chemical tricks that are so commonly used to separate one thing from another don’t work when you’re dealing with one kind of element, because chemically it’s all the same. You have to try to separate one thing from another based on something that’s different between the two.
Almost always that difference is mass. Lithium-6 has six units of atomic mass, lithium-7 has seven. Uranium-235 has 235 units of atomic mass, uranium-238 has 238. So there’s a difference there. It’s more pronounced for lithium than uranium, but it’s there nevertheless.
Separating uranium is a big deal because U-235 is fissile and U-238 is not. The original motivation to separate uranium was to make a bomb during the Manhattan Project. The first nuclear bomb ever used in war, 75 years ago today, was based on separated uranium-235. And enrichment has had a bad rap ever since.
To separate U-235 from U-238, you need to put them in a chemical form where it’s easier for them to get away from one another. Thank goodness for fluorine! Uranium hexafluoride (UF6) is a gaseous form of uranium. It has one uranium atom in the middle of six fluorine atoms. It looks a lot like one of those little jacks my sister used to play with. There’s another aspect to UF6 that’s really important. If fluorine itself had a number of different isotopes then this whole idea wouldn’t work. For instance, if there were isotopes of fluorine that had mass numbers of 18, 19, and 20, then you could go build a UF6 molecule and one of its fluorine’s might be 18, and another would be 20 and another could by 19, and that mass difference from uranium could get “lost in the noise” from all of the different isotopes of fluorine.
The crystal structure of This is a simple UF6 in a glass Ampoule
uranium hexafluoride (UF6) mononuclear molecule(UF6)
But fortunately, that’s not how it works. Fluorine has only one natural isotope, number 19. So when you go add six fluorine’s to uranium, you know that they’re all going to be 19. Any difference in mass from the molecule all comes from the uranium, not the fluorine. So we’ll do a little math. If you have a uranium atom that has a mass of 235, and you go and add six other atoms each with a mass of 19 to it, what do you get? (235 + 6*19) = 349. (I won’t lie, I used my calculator) And if you have a uranium atom with a mass of 238? (238 + 6*19) = 352.
So the whole trick in uranium enrichment is to separate molecules in a gas that have a mass of 349 from molecules that have a mass of 352. Folks, that’s not very much, and you can see why uranium enrichment is hard and expensive. But, thanks to the gaseous nature of uranium hexafluoride and the monoisotopic existence of fluorine, it’s possible in the first place, where otherwise it might not be.
Enrichment, part 2.
The basic equations that describe enrichment aren’t that hard to derive. Even you can do it! So here we go … :
You know that you’re going to start out with some amount of input material—the “feed” as it is called. You know that after you’re done you will have split the feed into two: the “product” and the waste, which in this case is called the “tails”. Assuming that you didn’t mess up and lose lots of material along the way, you could add up the product and the tails and that would be the same amount of material that you started with. So we’ll call the mass of the feed “mf”, we’ll call the mass of the product “mp”, and we’ll call the mass of the tails “mt”. And we’ll write a really simple equation that relates all three.
mf = mp + mt
Next, let’s assume that we have a mixture that has only two components. They might be U-235 and U-238, or Li-6 and Li-7, or Cl-35 and Cl-37. This derivation works for any two-component mixture. Let’s say that the fraction of the less abundant component (U-235 in the case of uranium) is given by a non-dimensional variable called “x”. And let’s say that that value of x is different for the feed, product, and tails. For instance, in the case of uranium, if the feed is natural uranium, 0.0071 of it is U-235. So the value for x for the feed would be 0.0071. xf = 0.0071. And let’s say that we want to make fuel for a light-water reactor out of this, and it needs the uranium enriched up to 3%, or 0.03. So the value of x for the “product” would be 0.03. xp = 0.03. The last thing to figure out would be how much U-235 we will tolerate in our “tails”, the part that we’re going to throw away.
At first blush, we might think, “hey, I don’t want to throw away any U-235, I want it to all go into my product. So I’ll set the tails to 0% and everything will be great.”
Hah—that seems like a good idea but it isn’t. Because the amount of effort it will take to strip every single last atom of U-235 from the mixture is infinite. So in reality don’t do that. So then you might think, “OK, that might be too hard, maybe I should set the tails enrichment higher so I don’t have to do as much work. I’ll set it to just a little bit less than the natural level of enrichment, something like 0.006%.”
Another bad idea. If you set the tails enrichment too low, you expend too much effort trying to get some small amount of stuff. If you set it too high, you end up throwing away most of the stuff you’re trying to get in the first place. So you have to be kind of careful about how you set your tails enrichment. Which will have everything to do with the economics of enrichment, as we shall see.
So I’ve spent this time telling you that you know the enrichment of the feed (easy, it’s the natural enrichment) and the enrichment of the product (easy, it’s what your customer wants) but the real question is what is the enrichment of your tails. That’s going to have to be a choice based on economics, and as economics change you might find yourself revisiting that decision.
OK, so let’s say we’ll set the tails enrichment at 0.003. xt = 0.003. That’s means about half of the U-235 in the original uranium is going to end up in your product and about half is going to end up in the tails. If we assume that the total amount of U-235 is constant, then we can write another equation:
xf*mf = xp*mp + xt*mt
This is just another way of saying that all of the U-235 ends up in either the product or the tails, and if you added it all up it would be the same as the amount that you had in the feed. Now we can combine these two equations to start figuring things out. We can use some of those tricks we learned in eighth-grade(4eme College) algebra to solve for things when we have two equations. We can rewrite the first equation to equal the tails rather than the feed:
mt = mf – mp
And we can substitute that definition into the second equation:
xf*mf = xp*mp + xt*(mf – mp)
Then, again using our eighth-grade(4eme College) algebra skills we can expand the equation:
xf*mf = xp*mp + xt*mf – xt*mp
and we can group the terms relating to the mass of the feed and the product:
xf*mf – xt*mf = xp*mp – xt*mp
We pull out the common factors…
mf*(xf – xt) = mp*(xp – xt)
…and then we can solve for the mass of the feed:
mf = mp*(xp – xt)/(xf – xt)
Or even better, we can figure out a ratio between the mass of the feed and the mass of the product:
mf/mp = (xp – xt)/(xf – xt)
Hooray! So why is this a big deal? Because now we have an answer that doesn’t really care how much actual mass of feed or product that we’re talking about. On the left-hand side of the equation is a ratio, and on the right-hand side of the equation are a bunch of enrichment values. Let me show you how useful this nifty little expression is.
Let’s say that you want to figure out how much natural uranium you will need to fuel a nuclear reactor that uses enriched uranium. This is pretty much the situation we are in in the World. Let’s say that you know that a typical reactor takes about 35 tonnes of enriched uranium fuel per year, and that that fuel is enriched up to 3%. You already know that the enrichment level of natural uranium is 0.0071, and let’s say that you’re comfortable with your tails enrichment being 0.003. So then you run the numbers:
mf/mp = (xp – xt)/(xf – xt) = (0.03 – 0.003)/(0.0071 – 0.003) = 0.027/0.0041 = 6.58
See how the tails enrichment shows up in both the numerator and the denominator of the expression? In this case, the ratio is 6.58, which tells you that you’ll need almost seven times more uranium as a feed material than you’ll need for fuel. So if you need 35 tonnes, you multiply 35*6.58 to get 230 tonnes. You’ll need 230 tonnes of natural uranium to make 35 tonnes of enriched uranium. Where does the rest of the uranium go? Into the tails. There’s 195 tonnes of uranium tails in this example. One of the things that you find when you do uranium calculations is that you almost always make a lot more tails than you make product.
But let’s do another example, to broaden our perspective. Let’s say that we’re talking about enriching lithium now instead of uranium. We want to make lithium-7 for a LFTR, and we need it to be enriched in lithium-7 up to a point of about 0.9999 (the more nines the better). But natural lithium is only about 90% enriched in lithium-7. So how much lithium feed will we need to enrich to 0.9999? Again, it has everything to do with the enrichment we’ll tolerate in the tails. Let’s say (being foolish) that we set the tails enrichment to 0.80. Don’t want to work too hard, right? So let’s go run the numbers and find a feed-to-product ratio for our lithium enrichment.
mf/mp = (xp – xt)/(xf – xt) = (0.9999 – 0.8)/(0.9 – 0.8) = 0.1999/0.1 = 1.999
In this case, we need about twice as much lithium feed to get a particular level of product. Why is that? Because by setting the tails to 0.8 only about half of the lithium-7 ended up in the product. The other half if in the tails. So even in a case where we have something like lithium-7, where it is the dominant constituent of natural lithium, setting the tails level of enrichment has a lot to do with how much feed it will take.
So let’s go back and run it again, this time with a tails enrichment of 0.5. No sense letting all that valuable lithium-7 go to waste, right?
mf/mp = (xp – xt)/(xf – xt) = (0.9999 – 0.5)/(0.9 – 0.5) = 0.1999/0.1 = 1.25
Now we have only a little bit more lithium feed (25%) than we expect as product—in other words, most of the lithium-7 ended up in our product stream rather than in the tails. Seems like a better way to go, right? Well, maybe. It still depends on a lot of other things, like how hard it actually is to do the separation.
Uranium Oxide Solar Panels, part 3.
Did you know that uranium dioxide is a semiconductor? In fact, it’s a really good one! That means that you could make solar panels, LEDs, and computer chips from it…can you imagine uranium oxide(nuclear waste) solar panels?

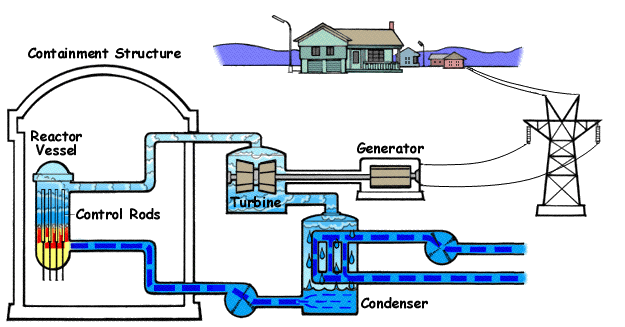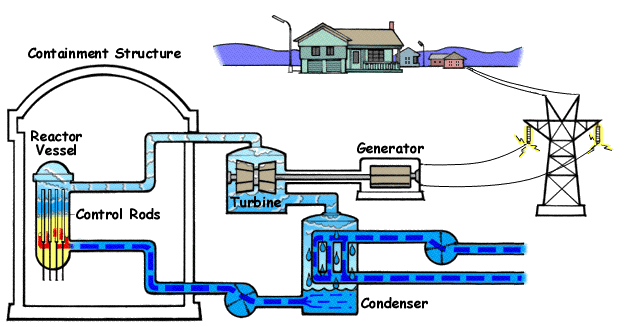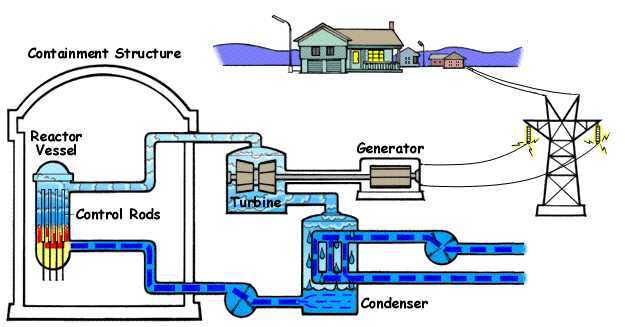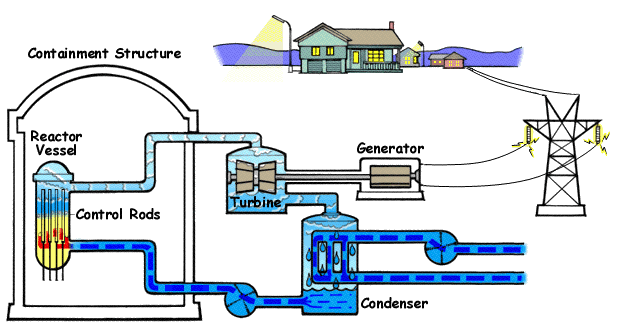
How a Nuclear Power Plant Work
Nuclear power plants run on uranium fuel. In the reactor, uranium atoms are split through a process known as fission(look above) When atoms are spilt, they produce a large amount of energy that is then converted to heat. The heat boils water, creating steam that is used to turn turbines, which spins the shaft of a generator. Inside the generator, coils of wire spin in a magnetic field and electricity is produced. Nuclear power plants in the United States use two types of reactors to achieve this process: pressurized water reactors(see animated PWR – just below) and boiling water reactors(see animated BWR – bottom of page).
The Pressurized Water Reactor (PWR)
Pressurized Water Reactors (PWR) keep water under pressure, so the water heats but does not boil. The heated pressurized water is run through pipes, which heat a separate water line to create steam. The water to generate steam is never mixed with the pressurized water used to heat it.
Boiling Water Reactor (BWR)
Boiling Water Reactors (BWR) heat water by generating heat from fission in the reactor vessel to boil water and create steam, which turns the generator. In both types of plants, the steam is turned back into water and can be used again in the process.
Courtesy of the Nuclear Regulatory Commission (NRC)

Left is the side view and under is the top view(for labels 1, 2 and 3)
1. Emergency stop bar – barre d’arrêt d’urgence
2. Control Bar – barre de contrôle
3. Fuel assembly – assemblage combustible
4. Biological protection – protection biologique
5. Steam outlet – sortie de vapeur
6. Water inlet – entrée de l’eau
7. Thermal protection – protection thermique
Boilling water reactor – réacteur à eau bouillante
the attachments to this page: